Fast (Fourier) multiplication

Figure 1: Representing the numbers 12 and 345 as frequency spectra,
 transforming them to time signals and multiplying.

One consequence of being able to convert between time signal and frequency spectrum representations is that they can be applied to the multiplication of multi-digit numbers in a way that is both straightforward and (potentially) quicker.

Consider the process of multiplying \(12\) by \(345\). I've fully expanded the intermediate steps with the colors representing the one's, ten's, hundred's and thousand's columns.

\[\begin{array}{r} 12\\ × \enspace 345\\ \hline \color{green}{10}\\ \color{red}{5}\enspace\\ _1 \color{red}{8}\enspace\\ \color{blue}{4}\enspace\enspace\\ _1 \color{blue}{6}\enspace\enspace\\ \color{goldenrod}{3}\enspace\enspace\enspace\\ \hline 4140 \end{array}\]

This operation is similarly represented in the following table where each number is separated into its digits and independently multiplied.

\( \begin{array}{|c|c|c|} \hline & & \color{gray}{10^1} & \color{gray}{10^0} \\ \hline & × & 1 & 2 \\ \hline \color{gray}{10^2} & 3 & \color{goldenrod}{3} & \color{blue}{6} \\ \hline \color{gray}{10^1} & 4 & \color{blue}{4} & \color{red}{8} \\ \hline \color{gray}{10^0} & 5 & \color{red}{5} & \color{green}{10} \\ \hline \end{array} \)

Calculating this, we get:

\(\begin{aligned}12 \cdot 345 & = (1  \!\cdot\!  {\color{gray}{10^1}} + 2  \!\cdot\!  {\color{gray}{10^0}})  \!\cdot\!  (3  \!\cdot\!  {\color{gray}{10^2}} + 4  \!\cdot\!  {\color{gray}{10^1}} + 5  \!\cdot\!  {\color{gray}{10^0}}) \\ & = 1  \!\cdot\!  {\color{gray}{10^1}}  \!\cdot\!  3  \!\cdot\!  {\color{gray}{10^2}} + 2  \!\cdot\!  {\color{gray}{10^0}}  \!\cdot\!  3  \!\cdot\!  {\color{gray}{10^2}} \, + \\ & \hspace{1.25em} 1  \!\cdot\!  {\color{gray}{10^1}}  \!\cdot\!  4  \!\cdot\!  {\color{gray}{10^1}} + 2  \!\cdot\!  {\color{gray}{10^0}}  \!\cdot\!  4  \!\cdot\!  {\color{gray}{10^1}} \, + \\ & \hspace{1.25em} 1  \!\cdot\!  {\color{gray}{10^1}}  \!\cdot\!  5  \!\cdot\!  {\color{gray}{10^0}} + 2  \!\cdot\!  {\color{gray}{10^0}}  \!\cdot\!  5  \!\cdot\!  {\color{gray}{10^0}} \\ & = {\color{goldenrod}{3}}  \!\cdot\!  {\color{gray}{10^3}} + {\color{blue}{6}}  \!\cdot\!  {\color{gray}{10^2}} + {\color{blue}{4}}  \!\cdot\!  {\color{gray}{10^2}} + {\color{red}{8}}  \!\cdot\!  {\color{gray}{10^1}} + {\color{red}{5}}  \!\cdot\!  {\color{gray}{10^1}} + {\color{green}{10}}  \!\cdot\!  {\color{gray}{10^0}} \\ & = {\color{goldenrod}{3}}  \!\cdot\!  {\color{gray}{10^3}} + ({\color{blue}{6}} + {\color{blue}{4}})  \!\cdot\!  {\color{gray}{10^2}} + ({\color{red}{8}} + {\color{red}{5}})  \!\cdot\!  {\color{gray}{10^1}} + {\color{green}{10}}  \!\cdot\!  {\color{gray}{10^0}} \\ & = {\color{goldenrod}{3}}  \!\cdot\!  {\color{gray}{10^3}} + {\color{blue}{10}}  \!\cdot\!  {\color{gray}{10^2}} + {\color{red}{13}}  \!\cdot\!  {\color{gray}{10^1}} + {\color{green}{10}}  \!\cdot\!  {\color{gray}{10^0}} \\ & = 4140 \end{aligned}\)

The coefficients \( [{\color{goldenrod}{3}}, {\color{blue}{10}}, {\color{red}{13}}, {\color{green}{10}}] \) are the convolution of \([1, 2]\) and \([3, 4, 5]\). Six component multiplications are required, thus performing in \( O(n^2) \) time.

A convolution can also be visualized as flipping the second number, sliding it under the first number, and accumulating products of corresponding digits along the way. For example, for \(12\) and \(345\):

  12    12     12    12

  ×     ××     ××     ×

543    543     543    543

-------------------------

  3     4      5      10

       + 6    + 8

-------------------------

  3     10     13     10

                

As before, six component multiplications are required.

However it so happens that if the numbers are each associated with a frequency spectrum (or, alternatively, a time signal), and transformed and multiplied in the dual domain then only four component multiplications are required, thus performing in \( O(n) \) time.[1]

Essentially, multiplying in the original domain (akin to standard multiplication) consists of multiplying digits and then adding the results. Whereas transforming and multiplying in the dual domain consists of adding digits and then multiplying the results.

As an analogy, consider how we might evaluate \((2 + 3) \cdot 7\). The multiplication-first approach is \(2 \cdot 7 + 3 \cdot 7 = 14 + 21 = 35\), requiring two multiplications. The multiplication-last approach is \((2 + 3) \cdot 7 = 5 \cdot 7 = 35\), requiring only one multiplication.

So how do we apply the multiplication-last approach for \(12 \cdot 345\)?

The first step is to represent each number as a frequency spectrum. The number \(12\) is represented as \([2, 1, 0, 0]\) and the number \(345\) is represented as \([5, 4, 3, 0]\). The digits are arranged in least-significant digit order, that is, by the one's digit first, then the ten's digit, and so on. They are also zero-padded to the output spectrum length which is equal to the total number of input digits minus one, that is, \(2 + 3 - 1 = 4\).

An inverse discrete Fourier transform is performed on each spectrum to produce their respective time signals:[2]

\(IDFT\,[2,1,0,0] = [3, 2+i, 1, 2-i]\)

\(IDFT\,[5,4,3,0] = [12, 2+4i, 4, 2-4i]\)

Next, each corresponding time sample is multiplied. This takes \(O(n)\) time.

\([3 \cdot 12, (2+i) \cdot (2+4i), 1 \cdot 4, (2-i) \cdot (2-4i)] = [36, 10i, 4, -10i]\)

A discrete Fourier transform is then performed to produce the final product spectrum (see Figure 1):[3]

\(DFT\,[36, 10i, 4, -10i] = [10, 13, 10, 3]\)

Flipping the order gives the coefficients \( [{\color{goldenrod}{3}}, {\color{blue}{10}}, {\color{red}{13}}, {\color{green}{10}}] \), therefore:

\( 12 \cdot 345 = {\color{goldenrod}{3}} \cdot {\color{gray}{10^3}} + {\color{blue}{10}} \cdot {\color{gray}{10^2}} + {\color{red}{13}} \cdot {\color{gray}{10^1}} + {\color{green}{10}} \cdot {\color{gray}{10^0}} = 4140 \)

The fastest algorithm for the IDFT/DFT is the fast Fourier transform which takes \(O(n\, log\, n)\) time and so the Fourier multiplication method improves on the conventional \(O(n^2)\) multiplication method for large numbers.

--

[1] The equivalence of convolution in the frequency domain and pointwise multiplication in the time domain (and vice-versa) is expressed by the convolution theorem.

Below is Python code for calculating the convolution and FFT-based multiplication for 12 and 345. Note that 1/4 scaling occurs in the forward transform (np.fft.fft).

import numpy as np

conv_result = np.convolve([1,2], [3,4,5])

print("Convolution:", conv_result.tolist())

fft_result = np.flip(np.fft.fft(np.fft.ifft(np.flip([0,0,1,2]), norm="forward") * np.fft.ifft(np.flip([0,3,4,5]), norm="forward"), norm="forward"))

print("FFT-based multiplication:", fft_result.real.astype(int).tolist())

Output:

Convolution: [3, 10, 13, 10]

FFT-based multiplication: [3, 10, 13, 10]

Note: if the numbers were represented as time signals rather than frequency spectra then the following line would be substituted (which switches the fft and ifft functions and defaults to norm="backward"). The output is identical.

fft_result = np.flip(np.fft.ifft(np.fft.fft(np.flip([0,0,1,2])) * np.fft.fft(np.flip([0,3,4,5]))))

[2] The math for the IDFT transforms is below. For each number, each digit is associated with a specific frequency over a time period - in this case, zero cycles for digits \(2\) and \(5\), one cycle for digits \(1\) and \(4\), and two cycles for digit \(3\). The resulting components of the IDFT transform are the samples at four regular points over the time period. To calculate the sample at each time point, each digit (as a complex amplitude) is rotated on the complex plane according to its associated frequency. In this case, the rotations are the fourth roots of unity: \(e^{2\pi ki/4}\) where \(k=0,1,2,3\) giving \(1, i, -1, -i\) (i.e., quarter turns from 1 on the complex unit circle).

\(\begin{aligned} IDFT\,[2,1,0,0] & = [2 \!\cdot\! 1 + 1 \!\cdot\! 1, \\ & \hspace{1.6em} 2 \!\cdot\! 1 + 1 \!\cdot\! i, \\ & \hspace{1.6em} 2 \!\cdot\! 1 + 1 \!\cdot\! -1, \\ & \hspace{1.6em} 2 \!\cdot\! 1 + 1 \!\cdot\! -i] \\ & \\ & = [2+1, \\ & \hspace{1.6em} 2+i, \\ & \hspace{1.6em} 2-1, \\ & \hspace{1.6em} 2-i] \\ & \\ & = [3, 2+i, 1, 2-i] \end{aligned}\)

For the initial time point no time has yet passed, so each digit remains unrotated (i.e., multiplied by \(1\)). At the second time point, digit \(2\) remains unrotated since its frequency is zero cycles and digit \(1\) is rotated by 90° (i.e., multiplied by \(i\)) since its frequency is one cycle. At the third time point, digit \(2\) remains unrotated and digit \(1\) is rotated by 180° (i.e., multiplied by \(-1\)). At the fourth time point, digit \(2\) remains unrotated and digit \(1\) is rotated by 270° (i.e., multiplied by \(-i\)).

\(\begin{aligned} IDFT\,[5,4,3,0] & = [5 \!\cdot\! 1 + 4 \!\cdot\! 1 + 3 \!\cdot\! 1, \\ & \hspace{1.6em} 5 \!\cdot\! 1 + 4 \!\cdot\! i + 3 \!\cdot\! -1, \\ & \hspace{1.6em} 5 \!\cdot\! 1 + 4 \!\cdot\! -1 + 3 \!\cdot\! 1, \\ & \hspace{1.6em} 5 \!\cdot\! 1 + 4 \!\cdot\! -i+3 \!\cdot\! -1] \\ & \\ & = [5+4+3, \\ & \hspace{1.6em} 5+4i-3, \\ & \hspace{1.6em} 5-4+3, \\ & \hspace{1.6em} 5-4i-3] \\ & \\ & = [12, 2+4i, 4, 2-4i] \end{aligned}\)

Similarly, for the initial time point no time has yet passed, so each digit remains unrotated (i.e., multiplied by \(1\)). At the second time point, digit \(5\) remains unrotated since its frequency is zero cycles, digit \(4\) is rotated by 90° (i.e., multiplied by \(i\)) since its frequency is one cycle and digit \(3\) is rotated by 180° (i.e., multiplied by \(-1\)) since its frequency is two cycles. At the third time point, each digit is rotated by 0°, 180° and 360° (or 0°) respectively. At the fourth time point, each digit is rotated by 0°, 270° (or -90°) and 540° (or 180°) respectively.

[3] The expanded math for the transforms and multiply operation.

\(DFT\,(IDFT\,[2,1,0,0] \cdot IDFT\,[5,4,3,0])\)

\(\begin{aligned}\hspace{0.8em} = \, DFT\,[ & (2 \!\cdot\! 1 + 1 \!\cdot\!  1)  \!\cdot\!   (5 \!\cdot\!  1 + 4 \!\cdot\!  1 + 3 \!\cdot\!  1), \\ & (2 \!\cdot\!  1 + 1 \!\cdot\!  i)  \!\cdot\!   (5 \!\cdot\!  1 + 4 \!\cdot\!  i + 3 \!\cdot\!  -1), \\ & (2 \!\cdot\!  1 + 1 \!\cdot\!  -1)  \!\cdot\!   (5 \!\cdot\!  1 + 4 \!\cdot\!  -1 + 3 \!\cdot\!  1), \\ & (2 \!\cdot\!  1 + 1 \!\cdot\!  -i)  \!\cdot\!   (5 \!\cdot\!  1 + 4 \!\cdot\!  -i + 3 \!\cdot\!  -1)] \\ & \\ =  \, DFT\,[ & (2 + 1) \!\cdot\! (5 + 4 + 3),\\ &  (2 + i) \!\cdot\! (5 + 4i -3),\\ &  (2 - 1) \!\cdot\! (5 - 4 + 3),\\ &  (2 - i) \!\cdot\! (5 - 4i - 3)]\end{aligned}\)

\(\begin{aligned}\hspace{0.6em} & = \, DFT\,[3 \cdot 12, (2+i) \cdot (2+4i), 1 \cdot 4, (2-i) \cdot (2-4i)] \\ & \\ & = \, DFT\,[36, 10i, 4, -10i]\end{aligned}\)

\(\begin{aligned}\hspace{0.8em} = \tfrac{1}{4} [ & 36 \!\cdot\! 1 + 10i \!\cdot\! 1 + 4 \!\cdot\! 1 - 10i \!\cdot\! 1, \\ & 36 \!\cdot\! 1 + 10i \!\cdot\! -i + 4 \!\cdot\! -1 - 10i \!\cdot\! i, \\ & 36 \!\cdot\! 1 + 10i \!\cdot\! -1 + 4 \!\cdot\! 1 - 10i \!\cdot\! -1, \\ & 36 \!\cdot\! 1 + 10i \!\cdot\! i + 4 \!\cdot\! -1 - 10i \!\cdot\! -i] \end{aligned}\)

\(\begin{aligned}\hspace{0.8em} = \tfrac{1}{4} [ & 36 + 10i + 4 - 10i, \\ & 36 + 10 - 4 + 10, \\ & 36 - 10i + 4 + 10i, \\ & 36 - 10 - 4 - 10] \end{aligned}\)

\(\begin{aligned}\hspace{0.8em} & = \tfrac{1}{4} [40, 52, 40, 12] \\ & \\ & = [10, 13, 10, 3]\end{aligned}\)

Visualizing the discrete Fourier transform

Figure 1: Yearly lunar satellite path (green)

In my earlier post, Visualizing von Neumann's elephant, I noted that the elephant drawing could be likened to a satellite's intricate movement through space. This analogy opens a window into understanding any signal's journey - not merely as a path traversed but as a choreography of circular motions, or epicycles. This dual perspective allows us to dissect a signal into its constituent frequencies (analysis) and, conversely, to construct complex paths from these foundational cycles (synthesis).

Per Figure 1, we're going to consider four bodies orbiting in space - the Sun, the Earth, the Moon and a lunar satellite.[1] The solid green path indicates the satellite's path through space over the course of each year. The large green dot marks the beginning of spring when the four bodies are aligned and the smaller green dots (in a counter-clockwise direction) indicate where the satellite will be at the beginning of summer, fall and winter.

I'll begin with the more intuitive synthesis process: constructing the satellite's path by tracking the bodies around their orbits. I'll then move onto the analysis process: recovering the initial positions of the bodies from the satellite's path. This is a way to visualize the mathematical operation of synthesizing a signal from a frequency spectrum (the inverse discrete Fourier transform) and, conversely, of analyzing a signal into its frequency components (the discrete Fourier transform).

Synthesis (the inverse discrete Fourier transform)

The first challenge is to calculate the position of the satellite at the beginning of each season (as marked by the green dots) from the orbit information. The initial relative positions of the four bodies are as follows:

1. The Sun is stationary. The Sun's position in space will be the origin (0,0) for the green dot coordinates.
2. The Earth is orbiting the Sun in an anti-clockwise direction at 1 cycle per year and its initial (x,y) coordinates are (20,0) relative to the Sun.
3. The Moon is orbiting the Earth in an anti-clockwise direction at 2 cycles per year and its initial coordinates are (12,0) relative to the Earth.
4. The satellite is orbiting the Moon in a clockwise direction at 1 cycle per year and its initial coordinates are (9,0) relative to the Moon.

The relative (x,y) coordinates can be encoded as a sequence of (potentially) complex numbers \([0, 20, 12, 9]\) where the sequential positions stand for the orbital frequencies of 0, 1, 2 and -1 cycles per year respectively. The sequence of complex numbers is, in effect, the frequency spectrum for the satellite time signal.[2]

Figure 2: Spring, summer, fall, winter, spring
(the satellite time signal is derived from
the initial relative body positions)

To calculate the satellite's position at the beginning of spring (see the first image in Figure 2), we just sum the complex numbers. That is, t0 = 0 + 20 + 12 + 9 = 41 (as indicated on the axes in Figure 1).

To generalize this procedure just a little, I will create a second sequence of complex numbers (called a basis vector) that represents just how much each body has rotated from its initial position. Each element will have an orbit radius length of 1 instead of the body's specific orbit radius length. The real value 1 will indicate no rotation, the imaginary value i will indicate a quarter anti-clockwise rotation, the real value -1 will indicate a half rotation and the imaginary value -i will indicate a three-quarter anti-clockwise rotation (or, conversely, a quarter clockwise rotation). In this case, the basis vector will be \([1, 1, 1, 1]\) since none of the bodies have yet rotated.

Our procedure will also include an operation called the dot product that takes two equal-length vectors (in this case, the basis vector and frequency vector), multiplies their corresponding elements and sums the products. That is, t0 = 1*0 + 1*20 + 1*12 + 1*9 = 41 which is the same result we intuitively reached above.

To calculate the satellite position at the beginning of summer (see the second image in Figure 2), we need to first calculate the relative position of each body after a season has passed. The Sun is stationary, so its (x,y) position remains as (0,0). The Earth has moved a quarter cycle around the Sun, so its position is now (0,20) relative to the Sun. The Moon has moved a half cycle around the Earth (since 2 cycles over the year divided by 4 is 1/2), so its position is now (-12,0) relative to the Earth. The satellite has moved a quarter cycle clockwise around the Moon, so its position is now (0,-9) relative to the Moon.

Now that we have all the relative positions, we can encode them as complex numbers and just sum as before. That is, t1 = 0 + 20i - 12 - 9i = -12 + 11i. Notice how we're really just tracing the path of the arrows from the Sun to the satellite, updating our coordinate position as we go.

In terms of our basis vector which represents the phase rotations but not the specific magnitudes, we have \([1, i, -1, -i]\) for 0, 1/4, 1/2 and -1/4 cycles respectively. Applying the dot product, we have 1*0 + i*20 - 1*12 - i*9 = 0 + 20i - 12 - 9i = -12 + 11i, as expected.

We continue this procedure for the beginning of fall and the beginning of winter (see the third and fourth images in Figure 2), which gives us t2 = -17 and t3 = -12 - 11i respectively. If we further calculate the satellite position for the beginning of next spring (see the fifth image in Figure 2), we get t4 = 41 which, not surprisingly, is the same as t0. A full year passes and a new cycle begins.

Collating our results, we have the sequence of complex numbers \([41, -12 + 11i, -17, -12 - 11i]\). This procedure is the inverse discrete Fourier transform (IDFT). We've synthesized the frequency spectrum (the initial spatial orbits and positions that the satellite's movement depends on) into a time signal (the seasonal satellite positions).

To streamline this procedure further, the basis vectors for calculating the time signal can be combined (column wise) into a matrix \(B^{-1}\), as follows:

\(B^{-1} = \begin{bmatrix}1 & 1 & 1 & 1\\1 & i & -1 & -i\\1 & -1 & 1 & -1\\1 & -i & -1 & i\end{bmatrix}\)

The IDFT formula becomes simply \(T = FB^{-1}\), where \(T\) is the time signal, \(F\) is the frequency spectrum and \(B^{-1}\) is the transformation basis matrix that describes the specific rotations for each body and time interval (in this case, four bodies and four seasons).

Synthesis: To calculate a seasonal satellite position, rotate the bodies up to that season from their initial relative positions and sum their resulting relative positions. More generally, to calculate the signal amplitude at a particular time, rotate the initial frequency amplitudes over that time and sum the resulting amplitudes.

Analysis (the discrete Fourier transform)

The second challenge, going in the reverse direction, is to calculate the orbit information from the satellite signal \([41, -12 + 11i, -17, -12 - 11i]\).

Figure 3: Sun, Earth, Moon, satellite
(the initial relative body positions are
derived from the satellite time signal)

To calculate the Sun's initial position (see the first image in Figure 3), we just average the complex numbers. That is, f0 = (41) / 4 + (-12 + 11i) / 4 + (-17) / 4 + (-12 - 11i) / 4 = (10.25) + (-3 + 2.75i) + (-4.25) + (-3 - 2.75i) = 0.[3]

Why does this work? Each of the other bodies move uniformly around a circle and so their positions cancel out.[4] What is left over is the Sun's initial position multiplied by four, since the Sun's initial position is factored into each of the satellite positions at the beginning of each season.[5]

Similar to the first challenge, I will create a second sequence of complex numbers (the basis vector) that represents how much the body being analyzed would need to rotate at the beginning of each season to return to its initial position at the beginning of spring. In this case, the basis vector will be \([1, 1, 1, 1]\) since the Sun does not rotate in any of the seasons.

Applying the dot product and then dividing by four, we have f0 = ((1*41 + 1*(-12 + 11i) - 1*17 + 1*(-12 - 11i)) / 4 = 0 which is the same result as above.

To calculate the Earth's initial position (see the second image in Figure 3), we first need to rotate each seasonal satellite position so that the Earth is in its initial position. At the beginning of spring, the Earth has not moved, so no rotation of the spring satellite position is needed. By summer, the Earth has moved a quarter cycle anti-clockwise, so we rotate the summer satellite position a quarter cycle clockwise. By fall, the Earth has moved a half cycle anti-clockwise, so we rotate the fall satellite position a half cycle clockwise. Finally, by winter, the Earth has moved three quarters of a cycle anti-clockwise, so we rotate the winter satellite position three quarters of a cycle clockwise (or, more simply, a quarter cycle anti-clockwise). The list of complex numbers after these rotations is \([41, 11 + 12i, 17, 11 - 12i]\). You can visualize the satellite at those positions by rotating each image in Figure 2 clockwise by a zero, quarter, half, three-quarter (and full) turn respectively.

Now we just average the complex numbers as we did with the Sun. That is, f1 = (41) / 4 + (11 + 12i) / 4 + (17) / 4 + (11 - 12i) / 4 = (10.25) + (2.75 + 3i) + (4.25) + (2.75 - 3i) = 20.  In effect, each body is represented as orbiting at one less cycle per year. This represents the Earth as stationary with the positions of the remaining uniformly moving bodies canceling out (i.e., the spectrum would be \([20, 12, 9, 0]\)).

In terms of our basis vector, we have \([1, -i, -1, i]\). Applying the dot product and 1/4 scaling to the original time signal, we have f1 = ((1*41 - i*(-12 + 11i) - 1*-17 + i*(-12 - 11i)) / 4 = 20, as expected.

We continue this procedure for the Moon and the satellite (see the third and fourth images in Figure 3), which gives us f2 = 12 and f3 = 9 respectively.

Collating our results, we have the sequence of complex numbers \([0, 20, 12, 9]\) which is the satellite spectrum that we started with. This procedure is the discrete Fourier transform (DFT). We've analyzed the time signal (the seasonal satellite positions) into a frequency spectrum (the initial spatial orbits and positions that the satellite's movement depends on).

As with the earlier IDFT, the basis vectors for calculating the time signal can be combined (column wise) into a matrix. When we include, for completion, the 1/4 scaling factor, the matrix becomes the inverse of \(B^{-1}\), as follows:[6]

\(B = \dfrac{1}{4}\begin{bmatrix}1 & 1 & 1 & 1\\1 & -i & -1 & i\\1 & -1 & 1 & -1\\1 & i & -1 & -i\end{bmatrix}\)

Thus, the DFT formula is \(F = TB\), where \(F\) is the frequency spectrum, \(T\) is the time signal and \(B\) is the transformation basis matrix that describes the specific (reverse) rotations for each body and time interval (in this case, four bodies and four seasons).

Analysis: To calculate a body's initial relative position, rotate each seasonal satellite position back by the amount that the body has rotated up to that season and average the resulting satellite positions. More generally, to calculate an initial frequency amplitude, rotate each time signal amplitude back by that frequency over that time period and average the resulting amplitudes.

Summary

To calculate a signal component (using the inverse DFT), each spectrum component is rotated by its frequency over that signal time period and then the products are summed. That is, we're constructing a signal from a spectrum.

Conversely, to calculate a spectrum component (using the DFT), each signal component is inversely rotated over its time period by that spectrum frequency and then the products are averaged. That is, we're retracing our steps to recover the spectrum from the signal.

For a different range of frequencies and time points, change the size of the square matrix and calculate the rotations.[7][8]

That's the discrete Fourier transform in a nutshell.[9][10]

Useful References

An Interactive Guide To The Fourier Transform - Better Explained

"The big insight: our signal is just a bunch of time spikes! If we merge the recipes for each time spike, we should get the recipe for the full signal."

Thanksgiving: The Fourier Transform  - Sean Carroll

"Fourier transforms are just a fancy version of changes of coordinates."

Intuitive Guide to Fourier Analysis: ch1, ch2, ch3, ch6 - Langton, Levin

Fourier Analysis - Steve Brunton, YouTube

Signals & Systems 2020 - Andrew Reader, YouTube

Seeing Circles, Sines and Signals - Jack Schaedler

Footnotes

[1] This is an epicycle model where the orbits are circular and uniform (and not affected by gravity).

The satellite example incorporates four frequencies (the initial relative positions and orbits of the Sun, Earth, Moon and satellite) and four time periods (the quarterly seasons - spring, summer, fall and winter). More generally, any natural number of equal frequency/period combinations can potentially be used. See footnote [7] for how that number is incorporated in the equations.

[2] The orbital frequencies {0, 1, 2 and -1} have been chosen to correspond to the frequencies for a 4x4 DFT matrix which includes negative frequencies. With four satellite measurements, a frequency of -1 is indistinguishable from a frequency of 3.

Note that it's straightforward to specify different initial relative positions for the bodies such as offsetting the Sun from the origin or setting a different phase for the Moon (by specifying different complex numbers).

While difficult to visualize, the complex numbers representing the relative coordinates for each of the four bodies can be considered to lie on mutually perpendicular axes, thus comprising a four-dimensional complex system.

[3] The time signal complex numbers are divided by 4 before the addition so that the components of the equation correspond with the component coordinates in Figure 3. The equation could be simplified and optimized by calculating the average after the addition. However this is an example of where doing so can easily make the visualization opaque.

[4] For example, the Earth is at coordinate (20, 0) in spring and (-20, 0) in the fall, so those positions cancel each other out. Similarly, the Earth is at coordinate (0, 20) in summer and (0, -20) in winter, so those positions also cancel each other out. See footnote [8] for how that cancelling shows up in the equations (at the line "\(= 4F_0\)").

[5] In other words, there is a signal spike (or Dirac delta function) for the position of the stationary body and a zero signal for the other body positions (which cancel out).

[6] Note that I divide by 4 in the DFT, not the IDFT, while Wikipedia uses the opposite convention. For a useful discussion on the conventions for rotation signs and normalization factors, see DFT - Why are the definitions for inverse and forward commonly switched?

[7] The basis matrices in this post use the fourth roots of unity which are 1, i, -1, and -i, that is, quarter turns from 1 on the complex unit circle. N roots can be derived by using \(e^{i (2\pi/N) k}\) where k = 0 to N - 1.

Given \(T\) is the \(N\times1\) time series, \(F\) is the \(N\times1\) frequency series, \(B\) is the \(N\times N\) DFT basis matrix (with \(B^{-1}\) the inverse DFT basis matrix) then:

\[T = F B^{-1}\]

\[F = T B\]

For a specific time signal or frequency spectrum component, the formulae are:

\[T_t = \sum_{f=0}^{N-1} F_f \cdot e^{i (2\pi / N) t f}\]

\[F_f = \frac{1}{N} \sum_{t=0}^{N-1} T_t \cdot e^{-i (2\pi / N) f t}\]

[8] The transform can also be extended to two or more dimensions. To compute a 2D DFT for four time points, create a 4x4 matrix for the 2D time signal. Compute the 1D DFT for each row to create an interim matrix \(M_{2D}\). Then compute the 1D DFT for each column in \(M_{2D}\) to create the 2D frequency spectrum. The columns represent the cycles in the first dimension (0, 1, 2 and -1) and the rows represent the cycles in the second dimension (also 0, 1, 2 and -1).

In the example below, the time signal \(T_{2D}\) starts at 1 (the top-left cell) and spins at 1 cycle per unit time in the horizontal direction and 2 cycles per unit time in the vertical direction. After applying the 2D DFT, the frequency spectrum \(F_{2D}\) has a spike in the cell at the second column and the third row, representing 1 cycle in the horizontal dimension and 2 cycles in the vertical dimension, as expected.

\(T_{2D} = \begin{bmatrix}1 & i & -1 & -i\\-1 & -i & 1 & i\\1 & i & -1 & -i\\-1 & -i & 1 & i\end{bmatrix} M_{2D} = \begin{bmatrix}0 & 1 & 0 & 0\\0 & -1 & 0 & 0\\0 & 1 & 0 & 0\\0 & -1 & 0 & 0\end{bmatrix} F_{2D} = \begin{bmatrix}0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 0 & 0\end{bmatrix} \)

[9] Given the required rotations 1, i, -1 and -i on the complex plane, the following equations calculate the IDFT (frequency spectrum to time samples) and DFT (time samples to frequency spectrum) respectively for the satellite path and cycles.

Calculating time samples \(T\) from frequency spectrum \(F = [0, 20, 12, 9]\)

\(\begin{aligned}T_0 & = F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1 \\ & = 0 + 20 + 12 + 9 \\ & = 41 \end{aligned}\)

\(\begin{aligned}T_1 & = F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i \\ & = 0 + 20i - 12 - 9i \\ & = -12 + 11i\end{aligned}\)

\(\begin{aligned}T_2 & = F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1 \\ & = 0 - 20 + 12 - 9 \\ & = -17\end{aligned}\)

\(\begin{aligned}T_3 & = F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i \\ & = 0 - 20i - 12 + 9i \\ & = -12 - 11i\end{aligned}\)

∴ \(T = [41, -12+11i, -17, -12-11i]\)

Calculating frequency spectrum \(F\) from time samples \(T = [41, -12+11i, -17, -12-11i]\)

\(\begin{aligned}T_0 * 1 + T_1 * 1 + T_2 * 1 + T_3 * 1 = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i) * 1 +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1)  * 1+\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * 1\\ & = 4F_0\end{aligned}\)

\(\begin{aligned}T_0 * 1 + T_1 * -i + T_2 * -1 + T_3 * i = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i) * -i +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1) * -1 +\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * i\\ & = 4F_1\end{aligned}\)

\(\begin{aligned}T_0 * 1 + T_1 * -1 + T_2 * 1 + T_3 * -1 = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i) * -1 +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1) * 1 +\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * -1\\ & = 4F_2\end{aligned}\)

\(\begin{aligned}T_0 * 1 + T_1 * i + T_2 * -1 + T_3 * -i = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * i) * -i +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1) * -1 +\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * -i\\ & = 4F_3\end{aligned}\)

\(\begin{aligned}F_0 & = \frac{1}{4}(T_0 * 1 + T_1 * 1 + T_2 * 1 + T_3 * 1) \\ & = 41 * 1 + (-12 + 11i) * 1 + -17 * 1 + (-12 - 11i) * 1 \\ & = 0 \end{aligned}\)

\(\begin{aligned}F_1 & = \frac{1}{4}(T_0 * 1 + T_1 * -i + T_2 * -1 + T_3 * i) \\ & = 41 * 1 + (-12 + 11i) * -i + -17 * -1 + (-12 - 11i) * i \\ & = 20 \end{aligned}\)

\(\begin{aligned}F_2 & = \frac{1}{4}(T_0 * 1 + T_1 * -1 + T_2 * 1 + T_3 * -1) \\ & = 41 * 1 + (-12 + 11i) * -1 + -17 * 1 + (-12 - 11i) * -1 \\ & = 12 \end{aligned}\)

\(\begin{aligned}F_3 & = \frac{1}{4}(T_0 * 1 + T_1 * i + T_2 * -1 + T_3 * -i) \\ & = 41 * 1 + (-12 + 11i) * i + -17 * -1 + (-12 - 11i) * -i \\ & = 9 \end{aligned}\)

∴ \(F = [0, 20, 12, 9]\)

[10] In the following visualizations, the epicycles are centered on the origin rather than cumulative. The orbit radiuses and consequent time signal remain unchanged.

The images on the left side of Figure 4 show the "side-on" time series for the real and imaginary dimensions. Note how the orbit radiuses add at each point in time to produce the time signal. The upper-right image shows the complex plane perspective (compare with Figure 1).  The lower-right image shows a 3D perspective where the the sinusoidal component waves wind around the time axis like a corkscrew.

Figure 4: Synthesis: the solid green time signal is the sum of the component sine waves that represent the motions of the orbiting bodies

Figure 5 shows the epicycles after multiplying the time signal in Figure 4 by the sinusoidal basis vectors [1, 1, 1, 1], [1, -i, -1, i], [1, -1, 1, -1] and [1, i, 1, -i] respectively. Note that these transformations return the Sun, Earth, Moon and satellite to their initial position in each respective image, thus representing them as stationary over time, with the remaining bodies in orbit. (The Sun is also stationary in each image because its orbit radius happens to be 0.) When the transformed time points are averaged in each image, the orbiting body positions cancel out revealing the initial position of the Sun, Earth, Moon and satellite respectively.

Figure 5: Analysis: the orbit positions in each transformed image cancel out revealing the position of the stationary body

Dissecting von Neumann's elephant

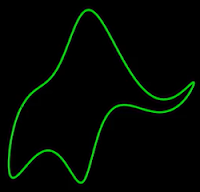Figure 1: Von Neumann's elephant

In my previous post, I quoted John von Neumann:

"With four parameters I can fit an elephant, and with five I can make him wiggle his trunk."

The goal of this post is to show how the elephant image in Figure 1 can be generated from just four complex parameters.[1]

As noted in my last post, the elephant can be regarded as a time signal that is produced using eight epicycles (illustrated in Figure 2). Each epicycle requires one complex value to encode both the length of its rotating radius and its starting angle.

To proceed with our goal, the first step is to extract a suitable number of (x, y) coordinates that represent the time signal. The green dots in Figure 2 (and Figure 3) show 16 coordinates on the complex plane which, proceeding clockwise from the left, are:

Figure 2: Epicycles and coordinates

t0: -60 + 2i

t1: -40.3703 + 21.9123i

t2: -22.1421 + 51.9411i

t3: -4.72831 + 82.9428i

t4: 20 + 50i

t5: 52.5074 + 9.44519i

t6: 78.7107 + 18.7696i

t7: 81.8089 + 16.356i

t8: 60 - 2i

t9: 29.0566 + 3.54352i

t10: 6.14214 - 15.9411i

t11: -6.5854 - 57.4869i

t12: -20 - 50i

t13: -41.1937 - 34.901i

t14: -62.7107 - 54.7696i

t15: -70.4952 - 41.8119i

Figure 3: Signal timeline (side-on) and complex plane (front-on) viewpoints

The next step is to rotate [2] and then split the signal into two separate signals derived from the real components and imaginary components respectively (i.e., {-2, -21.9123, ...} and {-60, -40.3703, ...}).

A Discrete Fourier Transform is now applied to each signal to produce their spectrums.[3][4] The first generated spectrum is:

f1: 50i

f2: 18i

f3: 12

f5: -14

The second generated spectrum is:

f1: -60-30i

f2: 8i

f3: -10i

There are eight distinct real numbers across both spectrums which can be arranged into four complex parameters, as required!

p1: 50 - 30i

p2: 18 +  8i

p3: 12 - 10i

p4: -14 - 60i

To check these parameters are sufficient to generate the elephant in Figure 1, the inverse procedure can be performed. First, the components of the four parameters specify the two spectrums above. An Inverse Discrete Fourier Transform is then applied to each spectrum to produce their respective signals. The real values of the two signals can then be combined into the original complex signal (and the inverse rotation applied) for the elephant in Figure 1.

One further (fifth) parameter is needed to add some elephant dynamics. The Mayer paper uses the number 40 to specify the x-coordinate of the base of the elephant's trunk (thus the coordinates to the right can be wiggled) and uses the number 20 to specify both the x and y coordinates of the elephant's eye. See the references in my earlier post for implementations of those features.

I'll end here with an apt paraphrase of Einstein: [5]

"Everything should be made as simple as possible (but not simpler)."

--

[1] See Drawing an elephant with four complex parameters - Mayer, Khairy, Howard, 2010.

[2] Note that the imaginary numbers have been negated and then the real and imaginary numbers swapped. This is, in effect, a quarter clockwise rotation of the signal which could alternatively be applied by multiplying the complex signal by i. The rotation isn't actually necessary to produce four parameters but, if omitted, the parameter values will be different from those given in the Mayer paper. The final four parameters without the rotation would be {30 + 50i, -8 + 18i, 10 - 12i, -60 + 14i}.

[3] Scaling factors have been omitted. When testing this using Microsoft Excel's Fourier Analysis tool, a scaling factor of 1/16 was needed for the DFT and 16 for the inverse DFT.

[4] Negative frequencies and zero amplitude frequencies have been omitted. A negative frequency means that an epicycle rotates clockwise instead of counter-clockwise. In this instance, the negative frequencies are the complex conjugates of the positive frequencies and don't affect the results.

[5] "It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience." - Albert Einstein, "On the Method of Theoretical Physics", The Herbert Spencer Lecture, 1933.

Visualizing von Neumann's elephant

Figure 1: This is not an elephant

John von Neumann once remarked to fellow physicist Enrico Fermi: [1]

"With four parameters I can fit an elephant, and with five I can make him wiggle his trunk."

Von Neumann was pointing out the danger of relying on too many input parameters to model a data set - which may then fail to fit additional data or predict future observations.

Figure 2: 128 sample points

Consider the elephant image in Figure 1. How might we model it in order to draw it programmatically?

One approach would be to find a number of points on the green line, as per Figure 2, and then join the points with straight lines.

Figure 3: Satellite path in green

However the approach I'm going to take is to draw the elephant using circles or, more specifically, epicycles.

An epicycle is a circle that moves on the perimeter of another circle and is famously associated with Ptolemaic astronomy. Per Figure 3, imagine the Earth's orbit around the Sun as a large circle and the moon's orbit as a smaller circle on that large circle. Then consider, in turn, a satellite orbiting the moon and you have the idea of epicycles and the complicated absolute path that the satellite can take through space.[2]

The key insight is that the elephant drawing in Figure 1 is, in a sense, just like the complicated satellite path. It also can be represented as a series of circles moving on circles over time. The magic of transforming the set of sample points in Figure 2 into a set of spinning circles is achieved via a Fourier Transform. Figure 4 below shows the (partial) result of applying that transformation.

Figure 4: Drawing an elephant from 128 epicycles (zoomed-in detail on right)

The larger circles (with their radial arrow identifying the present position of their orbiting satellite) contribute the broad strokes of the drawing, so-to-speak, while the smaller circles provide the finer detail.

So can we use less than 128 epicycles? Certainly. The next step is to remove the circles that have minimal effect on the shape of the elephant. These will generally be the smaller circles. Here are the results.[3]

Figure 5: (top row) 50 epicycles, 20 epicycles, (bottom row) 16 epicycles, 8 epicycles

With fifty epicycles, the drawing is virtually indistinguishable from the original image, whereas eight epicycles is about as far as one can reduce to while still retaining recognizable elephant features.[4]

The next step is to figure out how to specify those eight epicycles with just four parameters. That will be explored in my next post.

References:

Drawing an elephant with four complex parameters - Mayer, Khairy, Howard, 2010

The Noisy Elephant - Lydia Nemec

How to fit an elephant - John D. Cook

A Winking Pink Elephant - Neil Gunther

https://github.com/jramirezpr/fourier-elephant - Juan Carlos Ramirez

--

[1] A meeting with Enrico Fermi (subtitled "How one intuitive physicist rescued a team from fruitless research.") - Freeman Dyson, Nature, 2004

'“There are two ways of doing calculations in theoretical physics”, [Fermi] said. “One way, and this is the way I prefer, is to have a clear physical picture of the process that you are calculating. The other way is to have a precise and self-consistent mathematical formalism. You have neither. ... To reach your calculated results, you had to introduce arbitrary cut-off procedures that are not based either on solid physics or on solid mathematics."

...

In desperation I asked Fermi whether he was not impressed by the agreement between our calculated numbers and his measured numbers. He replied, “How many arbitrary parameters did you use for your calculations?” I thought for a moment about our cut-off procedures and said, “Four.” He said, “I remember my friend Johnny von Neumann used to say, with four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” With that, the conversation was over.'

[2] The term planet means "wanderer" in Greek, expressing the fact that they are seen to move across the sky relative to the background stars.

[3] The "8 epicycles" result comes from the Mayer paper and involves some adjustments to the remaining epicycles.

[4] Drawing with just one circle would produce a circular elephant.

The CHSH game

Figure 1: Playing the CHSH game

Consider the following game (see Figure 1):

Alice and Bob are in separate rooms with no way to communicate with each other. A referee in each room randomly flips a coin which the players see. Each player responds by saying "+1" or "-1".

For Alice and Bob to win the game, their responses have to be the same if and only if at least one of the coins show heads. They can agree on a strategy beforehand.

The game is repeated many times. What classical strategy maximizes their probability for winning and what is that probability? Have a go at answering it, then check below.

The best strategy is for both players to ignore the coin and just say "+1" every time.[1] They will win 75% of the time on average, losing only when both coins are tails. Thus we can say that any classical strategy wins ≤ 75% of the time. In this context, that's called a Bell inequality.

Figure 2: Playing the CHSH game (quantum strategy)

Figure 3: Entangled particle pair

Now let's try a specific quantum strategy (see Figure 2). For each game, Alice and Bob share a single entangled particle pair (see Figure 3).

Alice and Bob agree beforehand to each measure their particle at an angle that depends on the coin flips. On heads, Alice's measurement angle will be 0°, on tails 45°. On heads, Bob's measurement angle will be 22.5°, on tails -22.5°. They each measure their particle and report the "+1" or "-1" result.[2]

In three of the cases, at least one of the coins will be heads and the difference in Alice and Bob's measurement angles is 22.5°. QM predicts that they will measure the same result cos²(22.5°) ≈ 85% of the time.[3] In the double-tails case, the difference in Alice and Bob's measurement angles is 67.5°. QM predicts that they will measure a different result sin²(67.5°) ≈ 85% of the time. Thus Alice and Bob win the game on average 85% of the time.

So the quantum strategy is better than the best possible classical strategy, violating the Bell inequality. That's Bell's Theorem (one of many variants). So at least one of the classical assumptions is incorrect (hidden variables, locality, or statistical independence).

---

As an alternative presentation of the CHSH inequality, consider the following two-qubit observable composed of the various single-qubit observables that Alice and Bob can measure.

O = A_HB_H + A_HB_T + A_TB_H – A_TB_T

Each term specifies the product of a particular pair of measurements that Alice and Bob perform. For example, suppose when Alice's coin was heads, she measured -1 (with the 0° angle measurement) and when Bob's coin was tails, he measured +1 (with the -22.5° measurement). Thus the product A_HB_T would be -1 * + 1 = -1. Since the measured values are always either +1 or -1, a product term must also be either +1 or -1.

Note that it's not possible to make the four measurements jointly because they don't commute. However let's assume that each of the measurement pairs do have definite values even if they are not measured. This assumption is called realism (or hidden variables). Let's further assume that no communication occurs between Alice and Bob's particle. This assumption is called locality.

Now consider that observable O can be factored as:

O = (A_H + A_T)B_H + (A_H - A_T)B_T

Note that one of the parenthesized quantities must be equal to zero. That's because Alice's two possible measurement results (±1) would either add to 0 (if different) or subtract to 0 (if equal). So the maximum possible value for observable O is 2. This equation (and inequality) can be written as:

|E(O)| = |E(A_HB_H) + E(A_HB_T) + E(A_TB_H) – E(A_TB_T)| ≤ 2

where E specifies the expectation value. The expectation value for observable O can be empirically determined by running the experiment many times (using a new entangled particle pair and coin pair each time) and then summing the expectation values for each term.

The formula for the expectation value is:

E(ab) = (+1)cos²(θ) + (-1)sin²(θ) = cos(2*θ)

where θ is the relative angle between Alice and Bob’s measurements. So:

|E(O)| = |E(22.5°) + E(22.5°) + E(22.5°) – E(67.5°)|

           = |1/√2 + 1/√2 + 1/√2 – -1/√2| = 2√2 ≈ 2.828 ≰ 2

thus violating the CHSH inequality.[4]

As noted with the CHSH game, the Bell inequality depends on three assumptions. The first is locality (or no spooky action at a distance), which means that Alice and Bob have no way of communicating and thus potentially influencing the results. The second is hidden variables (or realism or counterfactual definiteness or non-contextuality), which means that there are definite values for the spin angles even if measurements are not performed at those angles. The third is statistical independence (or free-will or no conspiracy), which means that the coin flips are random and independent.

--

References:

Introduction to Quantum Information Science Lecture Notes, Lecture 13: Hidden Variables, Bell’s Inequality, Lecture 14: Nonlocal Games - Scott Aaronson

Quantum Randomness - American Scientist, Scott Aaronson

Bell's Inequality: The weirdest theorem in the world | Nobel Prize 2022 - Qiskit (video)

Bell's Theorem - Brilliant

--

[1] Enumeration of all possible deterministic strategies for the CHSH game:

  ==================================
 | Strategy | Coin| Say | Win | Win |
 |          | A B | A B |     |  %  |
  ==================================
 |          | H H | + + | Yes |     |
 | Heads:+1 | H T | + + | Yes | 75% |
 | Tails:+1 | T H | + + | Yes |     |
 |          | T T | + + | No  |     |
  ----------+-----+-----+-----+-----
 |          | H H | - - | Yes |     |
 | Heads:-1 | H T | - - | Yes | 75% |
 | Tails:-1 | T H | - - | Yes |     |
 |          | T T | - - | No  |     |
  ----------+-----+-----+-----+-----
 |          | H H | + + | Yes |     |
 | Heads:+1 | H T | + - | No  | 25% |
 | Tails:-1 | T H | - + | No  |     |
 |          | T T | - - | No  |     |
  ----------+-----+-----+-----+-----
 |          | H H | - - | Yes |     |
 | Heads:-1 | H T | - + | No  | 25% |
 | Tails:+1 | T H | + - | No  |     |
 |          | T T | + + | No  |     |
  ================================== 

[2] Figure 4 shows the quantum circuit diagram that creates the Bell state and rotates Alice and Bob's axes for the A_HB_H measurement combination.

Figure 4: Quantum circuit

The state vector is:

\(\begin{aligned}\hspace{20 mm}|\Psi\rangle = 0.653|00\rangle - 0.271|01\rangle + 0.271|10\rangle + 0.653|11\rangle\end{aligned}\)

The results "+1" and "-1" map to the \(|0\rangle\) and \(|1\rangle\) basis states respectively. The terms that represent Alice and Bob getting the same results are the \(|00\rangle\) and \(|11\rangle\) terms. Squaring the amplitudes for those terms and adding them gives 85% which is the expected win percentage for the A_HB_H measurement combination.

To view the state vectors for each measurement combination, click on the circuit diagram link in Figure 4 and use the following rotations (which will produce the associated state vector):

A_HB_H =  0° |  22.5° = RY(0 * pi/8 * 2) | RY( 1 * pi/8 * 2)

\(\begin{aligned}\hspace{10 mm}|\Psi\rangle = 0.653|00\rangle - 0.271|01\rangle + 0.271|10\rangle + 0.653|11\rangle\end{aligned}\)

A_HB_T =  0° | -22.5° = RY(0 * pi/8 * 2) | RY(-1 * pi/8 * 2)

\(\begin{aligned}\hspace{10 mm}|\Psi\rangle = 0.653|00\rangle + 0.271|01\rangle - 0.271|10\rangle + 0.653|11\rangle\end{aligned}\)

A_TB_H = 45° |  22.5° = RY(2 * pi/8 * 2) | RY( 1 * pi/8 * 2)

\(\begin{aligned}\hspace{10 mm}|\Psi\rangle = 0.653|00\rangle + 0.271|01\rangle - 0.271|10\rangle + 0.653|11\rangle\end{aligned}\)

A_TB_T = 45° | -22.5° = RY(2 * pi/8 * 2) | RY(-1 * pi/8 * 2)

\(\begin{aligned}\hspace{10 mm}|\Psi\rangle = 0.271|00\rangle + 0.653|01\rangle - 0.653|10\rangle + 0.271|11\rangle\end{aligned}\)

Note that on the Bloch sphere representation, orthogonal vectors are antiparallel. So the RY multiplier is π/8 * 2 (45°) rather than just π/8 (22.5°) because RY will internally divide the angle by 2.

[3] The measurement bases for each angle are:

0° \(\begin{aligned}\hspace{14 mm}\{ |0\rangle, |1\rangle \}\end{aligned}\)

45° \(\begin{aligned}\hspace{12 mm}\{ |\frac{\pi}{4}\rangle, |\frac{3\pi}{4}\rangle \}\end{aligned}\)

22.5° \(\begin{aligned}\hspace{9 mm}\{ |\frac{\pi}{8}\rangle, |\frac{5\pi}{8}\rangle \}\end{aligned}\)

-22.5° \(\begin{aligned}\hspace{8 mm}\{ |-\frac{\pi}{8}\rangle, |\frac{3\pi}{8}\rangle \}\end{aligned}\)

where

\(\begin{aligned}\hspace{20 mm}|\frac{\pi}{4}\rangle = cos(\frac{\pi}{4})|0\rangle + sin(\frac{\pi}{4})|1\rangle, |3\frac{\pi}{4}\rangle = cos(3\frac{\pi}{4})|0\rangle + sin(3\frac{\pi}{4})|1\rangle\end{aligned}\)

\(\begin{aligned}\hspace{20 mm}|\frac{\pi}{8}\rangle = cos(\frac{\pi}{8})|0\rangle + sin(\frac{\pi}{8})|1\rangle, |5\frac{\pi}{8}\rangle = cos(5\frac{\pi}{8})|0\rangle + sin(5\frac{\pi}{8})|1\rangle\end{aligned}\)

\(\begin{aligned}\hspace{20 mm}|-\frac{\pi}{8}\rangle = cos(-\frac{\pi}{8})|0\rangle + sin(-\frac{\pi}{8})|1\rangle, |\frac{3\pi}{8}\rangle = cos(\frac{3\pi}{8})|0\rangle + sin(\frac{3\pi}{8})|1\rangle\end{aligned}\)

and (see calculator)

 \(\begin{aligned}\hspace{20 mm}cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2} = 0.7071..., sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2} = 0.7071... \end{aligned}\)

 \(\begin{aligned}\hspace{20 mm}cos(\frac{\pi}{8}) = \frac{\sqrt{2 + \sqrt{2}}}{2} = 0.9238..., sin(\frac{\pi}{8}) = \frac{\sqrt{2 - \sqrt{2}}}{2} = 0.3826... \end{aligned}\)

[4] The result 2√2 is also the Tsirelson bound, which is the upper limit of the Bell violation. The disparity between the classical and quantum predictions for detector angle differences is shown in Figure 5.

Figure 5: Classical and quantum predictions

Bell states and measurements

Figure 1: John Bell

The Bell states (named after physicist John Bell) are four maximally entangled quantum states of two qubits. This post describes the bell states and the quantum circuits for implementing them. Click on the circuit label to open in IBM Quantum Composer.

The four Bell states are:

Circuit 1:\(|\Phi^+\rangle\)

\(\begin{aligned}\hspace{20 mm}|\Phi^+\rangle = \frac{|00\rangle + |11\rangle}{\sqrt2}\end{aligned}\)

Circuit 2: \(|\Phi^-\rangle\)

\(\begin{aligned}\hspace{20 mm}|\Phi^-\rangle = \frac{|00\rangle - |11\rangle}{\sqrt2}\end{aligned}\)

Circuit 3: \(|\Psi^+\rangle\)

\(\begin{aligned}\hspace{20 mm}|\Psi^+\rangle = \frac{|01\rangle + |10\rangle}{\sqrt2}\end{aligned}\)

Circuit 4: \(|\Psi^-\rangle\)

\(\begin{aligned}\hspace{20 mm}|\Psi^-\rangle = \frac{|01\rangle - |10\rangle}{\sqrt2}\end{aligned}\)

All circuits are implemented with a Hadamard gate followed by a controlled NOT gate. Some circuits also utilize the Pauli-X (NOT) gate and Pauli-Z gate.[1]

Note that in some circuit editors, the Pauli-X gate may be rendered with a squared-X symbol rather than a circled-plus symbol as rendered here. Also, this is just one of many possible implementation of the Bell states.[2]

Measurements

By default, measurements are in the Z-basis.

To measure in the X-basis, use a Hadamard gate which rotates the state onto the X-axis.

Figure 2:  The Hadamard gate interchanges
the X- and Z-axes, and inverts the Y-axis

To measure in the Y-basis use an inverse S gate (S^†) followed by a Hadamard gate which rotates the state onto the Y-axis.

Figure 3: The S^† gate performs a quarter turn
clockwise about the Z-axis

The quantum circuits for measuring in the three Pauli bases:

Figure 4: Measuring in Pauli bases

--

[1] Description of circuits (where Z_n and X_n act on qubit q[n]):

\(\begin{aligned}\hspace{5 mm}|\Phi^+\rangle = CNOT \cdot H_0 |00 \rangle\end{aligned}\)

\(\begin{aligned}\hspace{5 mm}|\Phi^-\rangle = Z_1 \cdot CNOT \cdot H_0 |00 \rangle\end{aligned}\)

\(\begin{aligned}\hspace{5 mm}|\Psi^+\rangle = X_0 \cdot CNOT \cdot H_0 |00 \rangle\end{aligned}\)

\(\begin{aligned}\hspace{5 mm}|\Psi^-\rangle = X_0 \cdot Z_1 \cdot CNOT \cdot H_0 |00 \rangle\end{aligned}\)

[2] An alternative set of circuits for creating Bell states.

Figure 5: Alternative Bell state circuits