|
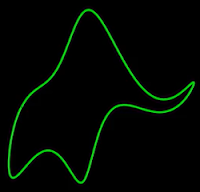
| Figure 1: Yearly lunar satellite path (green) |
In my earlier post,
Visualizing von Neumann's elephant, I noted that the elephant drawing could be likened to a satellite's intricate movement through space. This analogy opens a window into understanding any signal's journey - not merely as a path traversed but as a choreography of circular motions, or epicycles. This dual perspective allows us to dissect a signal into its constituent frequencies (analysis) and, conversely, to construct complex paths from these foundational cycles (synthesis).
Per Figure 1, we're going to consider four bodies orbiting in space - the Sun, the Earth, the Moon and a lunar satellite.[1] The solid green path indicates the satellite's path through space over the course of each year. The large green dot marks the beginning of spring when the four bodies are aligned and the smaller green dots (in a counter-clockwise direction) indicate where the satellite will be at the beginning of summer, fall and winter.
I'll begin with the more intuitive synthesis process: constructing the satellite's path by tracking the bodies around their orbits. I'll then move onto the analysis process: recovering the initial positions of the bodies from the satellite's path. This is a way to visualize the mathematical operation of synthesizing a signal from a frequency spectrum (the
inverse discrete Fourier transform) and, conversely, of analyzing a signal into its frequency components (the discrete Fourier transform).
Synthesis (the inverse discrete Fourier transform)
The first challenge is to calculate the position of the satellite at the beginning of each season (as marked by the green dots) from the orbit information. The initial relative positions of the four bodies are as follows:
- The Sun is stationary. The Sun's position in space will be the origin (0,0) for the green dot coordinates.
- The Earth is orbiting the Sun in an anti-clockwise direction at 1 cycle per year and its initial (x,y) coordinates are (20,0) relative to the Sun.
- The Moon is orbiting the Earth in an anti-clockwise direction at 2 cycles per year and its initial coordinates are (12,0) relative to the Earth.
- The satellite is orbiting the Moon in a clockwise direction at 1 cycle per year and its initial coordinates are (9,0) relative to the Moon.
The relative (x,y) coordinates can be encoded as a sequence of (potentially)
complex numbers \([0, 20, 12, 9]\) where the sequential positions stand for the orbital frequencies of 0, 1, 2 and -1 cycles per year respectively. The sequence of complex numbers is, in effect, the frequency spectrum for the satellite time signal.[2]
 |
Figure 2: Spring, summer, fall, winter, spring
(the satellite time signal is derived from
the initial relative body positions) |
To calculate the satellite's position at the beginning of spring (see the first image in
Figure 2), we just sum the complex numbers. That is, t0 = 0 + 20 + 12 + 9 = 41 (as indicated on the axes in
Figure 1).
To generalize this procedure just a little, I will create a second sequence of complex numbers (called a
basis vector) that represents just how much each body has rotated from its initial position. Each element will have an orbit radius length of 1 instead of the body's specific orbit radius length. The real value 1 will indicate no rotation, the imaginary value i will indicate a quarter anti-clockwise rotation, the real value -1 will indicate a half rotation and the imaginary value -i will indicate a three-quarter anti-clockwise rotation (or, conversely, a quarter clockwise rotation). In this case, the basis vector will be \([1, 1, 1, 1]\) since none of the bodies have yet rotated.
Our procedure will also include an operation called the
dot product that takes two equal-length vectors (in this case, the basis vector and frequency vector), multiplies their corresponding elements and sums the products. That is, t0 = 1*0 + 1*20 + 1*12 + 1*9 = 41 which is the same result we intuitively reached above.
To calculate the satellite position at the beginning of summer (see the second image in Figure 2), we need to first calculate the relative position of each body after a season has passed. The Sun is stationary, so its (x,y) position remains as (0,0). The Earth has moved a quarter cycle around the Sun, so its position is now (0,20) relative to the Sun. The Moon has moved a half cycle around the Earth (since 2 cycles over the year divided by 4 is 1/2), so its position is now (-12,0) relative to the Earth. The satellite has moved a quarter cycle clockwise around the Moon, so its position is now (0,-9) relative to the Moon.
Now that we have all the relative positions, we can encode them as complex numbers and just sum as before. That is, t1 = 0 + 20i - 12 - 9i = -12 + 11i. Notice how we're really just tracing the path of the arrows from the Sun to the satellite, updating our coordinate position as we go.
In terms of our basis vector which represents the phase rotations but not the specific magnitudes, we have \([1, i, -1, -i]\) for 0, 1/4, 1/2 and -1/4 cycles respectively. Applying the dot product, we have 1*0 + i*20 - 1*12 - i*9 = 0 + 20i - 12 - 9i = -12 + 11i, as expected.
We continue this procedure for the beginning of fall and the beginning of winter (see the third and fourth images in Figure 2), which gives us t2 = -17 and t3 = -12 - 11i respectively. If we further calculate the satellite position for the beginning of next spring (see the fifth image in Figure 2), we get t4 = 41 which, not surprisingly, is the same as t0. A full year passes and a new cycle begins.
Collating our results, we have the sequence of complex numbers \([41, -12 + 11i, -17, -12 - 11i]\). This procedure is the
inverse discrete Fourier transform (IDFT). We've synthesized the frequency spectrum (the initial spatial orbits and positions that the satellite's movement depends on) into a time signal (the seasonal satellite positions).
To streamline this procedure further, the basis vectors for calculating the time signal can be combined (column wise) into a matrix \(B^{-1}\), as follows:
\(B^{-1} = \begin{bmatrix}1 & 1 & 1 & 1\\1 & i & -1 & -i\\1 & -1 & 1 & -1\\1 & -i & -1 & i\end{bmatrix}\)
The IDFT formula becomes simply \(T = B^{-1}F\), where \(T\) is the time signal, \(F\) is the frequency spectrum and \(B^{-1}\) is the transformation basis matrix that describes the specific rotations for each body and time interval (in this case, four bodies and four seasons).
Synthesis: To calculate a seasonal satellite position, rotate the bodies up to that season from their initial relative positions and sum their resulting relative positions. More generally, to calculate the signal amplitude at a particular time, rotate the initial frequency amplitudes over that time and sum the resulting amplitudes.
Analysis (the discrete Fourier transform)
The second challenge, going in the reverse direction, is to calculate the orbit information from the satellite signal \([41, -12 + 11i, -17, -12 - 11i]\).
 |
Figure 3: Sun, Earth, Moon, satellite
(the initial relative body positions are
derived from the satellite time signal) |
To calculate the Sun's initial position (see the first image in
Figure 3), we just average the complex numbers. That is, f0 = (41) / 4 + (-12 + 11i) / 4 + (-17) / 4 + (-12 - 11i) / 4 = (
10.25) + (
-3 + 2.75i) + (
-4.25) + (
-3 - 2.75i) =
0.[3]
Why does this work? Each of the other bodies move uniformly around a circle and so their positions cancel out.[4] What is left over is the Sun's initial position multiplied by four, since the Sun's initial position is factored into each of the satellite positions at the beginning of each season.[5]
Similar to the first challenge, I will create a second sequence of complex numbers (the basis vector) that represents how much the body being analyzed would need to rotate at the beginning of each season to return to its initial position at the beginning of spring. In this case, the basis vector will be \([1, 1, 1, 1]\) since the Sun does not rotate in any of the seasons.
Applying the dot product and then dividing by four, we have f0 = ((1*41 + 1*(-12 + 11i) - 1*17 + 1*(-12 - 11i)) / 4 = 0 which is the same result as above.
To calculate the Earth's initial position (see the second image in Figure 3), we first need to rotate each seasonal satellite position so that the Earth is in its initial position. At the beginning of spring, the Earth has not moved, so no rotation of the spring satellite position is needed. By summer, the Earth has moved a quarter cycle anti-clockwise, so we rotate the summer satellite position a quarter cycle clockwise. By fall, the Earth has moved a half cycle anti-clockwise, so we rotate the fall satellite position a half cycle clockwise. Finally, by winter, the Earth has moved three quarters of a cycle anti-clockwise, so we rotate the winter satellite position three quarters of a cycle clockwise (or, more simply, a quarter cycle anti-clockwise). The list of complex numbers after these rotations is \([41, 11 + 12i, 17, 11 - 12i]\). You can visualize the satellite at those positions by rotating each image in Figure 2 clockwise by a zero, quarter, half, three-quarter (and full) turn respectively.
Now we just average the complex numbers as we did with the Sun. That is, f1 = (41) / 4 + (11 + 12i) / 4 + (17) / 4 + (11 - 12i) / 4 = (10.25) + (2.75 + 3i) + (4.25) + (2.75 - 3i) = 20. In effect, each body is represented as orbiting at one less cycle per year. This represents the Earth as stationary with the positions of the remaining uniformly moving bodies canceling out (i.e., the spectrum would be \([20, 12, 9, 0]\)).
In terms of our basis vector, we have \([1, -i, -1, i]\). Applying the dot product and 1/4 scaling to the original time signal, we have f1 = ((1*41 - i*(-12 + 11i) - 1*-17 + i*(-12 - 11i)) / 4 = 20, as expected.
We continue this procedure for the Moon and the satellite (see the third and fourth images in Figure 3), which gives us f2 = 12 and f3 = 9 respectively.
Collating our results, we have the sequence of complex numbers \([0, 20, 12, 9]\) which is the satellite spectrum that we started with. This procedure is the
discrete Fourier transform (DFT). We've analyzed the time signal (the seasonal satellite positions) into a frequency spectrum (the initial spatial orbits and positions that the satellite's movement depends on).
As with the earlier IDFT, the basis vectors for calculating the time signal can be combined (column wise) into a matrix. When we include, for completion, the 1/4 scaling factor, the matrix becomes the
inverse of \(B^{-1}\), as follows:[6]
\(B = \dfrac{1}{4}\begin{bmatrix}1 & 1 & 1 & 1\\1 & -i & -1 & i\\1 & -1 & 1 & -1\\1 & i & -1 & -i\end{bmatrix}\)
Thus, the DFT formula is \(F = BT\), where \(F\) is the frequency spectrum, \(T\) is the time signal and \(B\) is the transformation basis matrix that describes the specific (reverse) rotations for each body and time interval (in this case, four bodies and four seasons).
Analysis: To calculate a body's initial relative position, rotate each seasonal satellite position back by the amount that the body has rotated up to that season and average the resulting satellite positions. More generally, to calculate an initial frequency amplitude, rotate each time signal amplitude back by that frequency over that time period and average the resulting amplitudes.
Summary
To calculate a signal component (using the inverse DFT), each spectrum component is rotated by its frequency over that signal time period and then the products are summed. That is, we're constructing a signal from a spectrum.
Conversely, to calculate a spectrum component (using the DFT), each signal component is inversely rotated over its time period by that spectrum frequency and then the products are averaged. That is, we're retracing our steps to recover the spectrum from the signal.
For a different range of frequencies and time points, change the size of the square matrix and calculate the rotations.[7][8]
That's the discrete Fourier transform in a nutshell.[9][10]
Footnotes
[1] This is an epicycle model where the orbits are circular and uniform (and not affected by gravity).
The satellite example incorporates four frequencies (the initial relative positions and orbits of the Sun, Earth, Moon and satellite) and four time periods (the quarterly seasons - spring, summer, fall and winter). More generally, any natural number of equal frequency/period combinations can potentially be used. See footnote [7] for how that number is incorporated in the equations.
[2] The orbital frequencies {0, 1, 2 and -1} have been chosen to correspond to the frequencies for a 4x4
DFT matrix which includes
negative frequencies. With four satellite measurements, a frequency of -1 is
indistinguishable from a frequency of 3.
Note that it's straightforward to specify different initial relative positions for the bodies such as offsetting the Sun from the origin or setting a different phase for the Moon (by specifying different complex numbers).
While difficult to visualize, the complex numbers representing the relative coordinates for each of the four bodies can be considered to lie on mutually perpendicular axes, thus comprising a four-dimensional complex system.
[3] The time signal complex numbers are divided by 4
before the addition so that the components of the equation correspond with the component coordinates in
Figure 3. The equation could be simplified and optimized by calculating the average
after the addition. However this is an example of where doing so can easily make the visualization
opaque.
[4] For example, the Earth is at coordinate (20, 0) in spring and (-20, 0) in the fall, so those positions cancel each other out. Similarly, the Earth is at coordinate (0, 20) in summer and (0, -20) in winter, so those positions also cancel each other out. See footnote [8] for how that cancelling shows up in the equations (at the line "\(= 4F_0\)").
[5] In other words, there is a signal spike (or
Dirac delta function) for the position of the stationary body and a zero signal for the other body positions (which cancel out).
[7] The basis matrices in this post use the fourth
roots of unity which are 1, i, -1, and -i, that is, quarter turns from 1 on the complex unit circle. N roots can be derived by using \(e^{i (2\pi/N) k}\) where k = 0 to N - 1.
Given \(T\) is the \(N\times1\) time series, \(F\) is the \(N\times1\) frequency series, \(B\) is the \(N\times N\)
DFT basis matrix (with \(B^{-1}\) the inverse DFT basis matrix) then:
\[T = B^{-1} F\]
\[F = B T\]
For a specific time signal or frequency spectrum component, the formulae are:
\[T_t = \sum_{f=0}^{N-1} F_f \cdot e^{i (2\pi / N) t f}\]
\[F_f = \frac{1}{N} \sum_{t=0}^{N-1} T_t \cdot e^{-i (2\pi / N) f t}\]
[8] The transform can also be extended to two or more dimensions. To compute a 2D DFT for four time points, create a 4x4 matrix for the 2D time signal. Compute the 1D DFT for each row to create an interim matrix \(M_{2D}\). Then compute the 1D DFT for each column in \(M_{2D}\) to create the 2D frequency spectrum. The columns represent the cycles in the first dimension (0, 1, 2 and -1) and the rows represent the cycles in the second dimension (also 0, 1, 2 and -1).
In the example below, the time signal \(T_{2D}\) starts at 1 (the top-left cell) and spins at 1 cycle per unit time in the horizontal direction and 2 cycles per unit time in the vertical direction. After applying the 2D DFT, the frequency spectrum \(F_{2D}\) has a spike in the cell at the second column and the third row, representing 1 cycle in the horizontal dimension and 2 cycles in the vertical dimension, as expected.
\(T_{2D} = \begin{bmatrix}1 & i & -1 & -i\\-1 & -i & 1 & i\\1 & i & -1 & -i\\-1 & -i & 1 & i\end{bmatrix} M_{2D} = \begin{bmatrix}0 & 1 & 0 & 0\\0 & -1 & 0 & 0\\0 & 1 & 0 & 0\\0 & -1 & 0 & 0\end{bmatrix} F_{2D} = \begin{bmatrix}0 & 0 & 0 & 0\\0 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 0 & 0\end{bmatrix} \)
[9] Given the required rotations 1, i, -1 and -i on the complex plane, the following equations calculate the IDFT (frequency spectrum to time samples) and DFT (time samples to frequency spectrum) respectively for the satellite path and cycles.
Calculating time samples \(T\) from frequency spectrum \(F = [0, 20, 12, 9]\)
\(\begin{aligned}T_0 & = F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1 \\ & = 0 + 20 + 12 + 9 \\ & = 41 \end{aligned}\)
\(\begin{aligned}T_1 & = F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i \\ & = 0 + 20i - 12 - 9i \\ & = -12 + 11i\end{aligned}\)
\(\begin{aligned}T_2 & = F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1 \\ & = 0 - 20 + 12 - 9 \\ & = -17\end{aligned}\)
\(\begin{aligned}T_3 & = F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i \\ & = 0 - 20i - 12 + 9i \\ & = -12 - 11i\end{aligned}\)
∴ \(T = [41, -12+11i, -17, -12-11i]\)
Calculating frequency spectrum \(F\) from time samples \(T = [41, -12+11i, -17, -12-11i]\)
\(\begin{aligned}T_0 * 1 + T_1 * 1 + T_2 * 1 + T_3 * 1 = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i) * 1 +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1) * 1+\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * 1\\ & = 4F_0\end{aligned}\)
\(\begin{aligned}T_0 * 1 + T_1 * -i + T_2 * -1 + T_3 * i = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i) * -i +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1) * -1 +\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * i\\ & = 4F_1\end{aligned}\)
\(\begin{aligned}T_0 * 1 + T_1 * -1 + T_2 * 1 + T_3 * -1 = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * -i) * -1 +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1) * 1 +\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * -1\\ & = 4F_2\end{aligned}\)
\(\begin{aligned}T_0 * 1 + T_1 * i + T_2 * -1 + T_3 * -i = & (F_0 * 1 + F_1 * 1 + F_2 * 1 + F_3 * 1) * 1 +\\ & (F_0 * 1 + F_1 * i + F_2 * -1 + F_3 * i) * -i +\\ & (F_0 * 1 + F_1 * -1 + F_2 * 1 + F_3 * -1) * -1 +\\ & (F_0 * 1 + F_1 * -i + F_2 * -1 + F_3 * i) * -i\\ & = 4F_3\end{aligned}\)
\(\begin{aligned}F_0 & = \frac{1}{4}(T_0 * 1 + T_1 * 1 + T_2 * 1 + T_3 * 1) \\ & = 41 * 1 + (-12 + 11i) * 1 + -17 * 1 + (-12 - 11i) * 1 \\ & = 0 \end{aligned}\)
\(\begin{aligned}F_1 & = \frac{1}{4}(T_0 * 1 + T_1 * -i + T_2 * -1 + T_3 * i) \\ & = 41 * 1 + (-12 + 11i) * -i + -17 * -1 + (-12 - 11i) * i \\ & = 20 \end{aligned}\)
\(\begin{aligned}F_2 & = \frac{1}{4}(T_0 * 1 + T_1 * -1 + T_2 * 1 + T_3 * -1) \\ & = 41 * 1 + (-12 + 11i) * -1 + -17 * 1 + (-12 - 11i) * -1 \\ & = 12 \end{aligned}\)
\(\begin{aligned}F_3 & = \frac{1}{4}(T_0 * 1 + T_1 * i + T_2 * -1 + T_3 * -i) \\ & = 41 * 1 + (-12 + 11i) * i + -17 * -1 + (-12 - 11i) * -i \\ & = 9 \end{aligned}\)
∴ \(F = [0, 20, 12, 9]\)
[10] In the following visualizations, the epicycles are centered on the origin rather than cumulative. The orbit radiuses and consequent time signal remain unchanged.
The images on the left side of Figure 4 show the "side-on" time series for the real and imaginary dimensions. Note how the orbit radiuses add at each point in time to produce the time signal. The upper-right image shows the complex plane perspective (compare with Figure 1). The lower-right image shows a 3D perspective where the the sinusoidal component waves wind around the time axis like a corkscrew.
 |
| Figure 4: Synthesis: the solid green time signal is the sum of the component sine waves that represent the motions of the orbiting bodies |
Figure 5 shows the epicycles after multiplying the time signal in Figure 4 by the sinusoidal basis vectors [1, 1, 1, 1], [1, -i, -1, i], [1, -1, 1, -1] and [1, i, 1, -i] respectively. Note that these transformations return the Sun, Earth, Moon and satellite to their initial position in each respective image, thus representing them as stationary over time, with the remaining bodies in orbit. (The Sun is also stationary in each image because its orbit radius happens to be 0.) When the transformed time points are averaged in each image, the orbiting body positions cancel out revealing the initial position of the Sun, Earth, Moon and satellite respectively.
 |
| Figure 5: Analysis: the orbit positions in each transformed image cancel out revealing the position of the stationary body |