Dissecting von Neumann's elephant

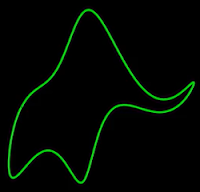
Figure 1: Von Neumann's elephant

In my previous post, I quoted John von Neumann:

"With four parameters I can fit an elephant, and with five I can make him wiggle his trunk."

The goal of this post is to show how the elephant image in Figure 1 can be generated from just four complex parameters.[1]

As noted in my last post, the elephant can be regarded as a time signal that is produced using eight epicycles (illustrated in Figure 2). Each epicycle requires one complex value to encode both the length of its rotating radius and its starting angle.

To proceed with our goal, the first step is to extract a suitable number of (x, y) coordinates that represent the time signal. The green dots in Figure 2 (and Figure 3) show 16 coordinates on the complex plane which, proceeding clockwise from the left, are:

Figure 2: Epicycles and coordinates

t0: -60 + 2i

t1: -40.3703 + 21.9123i

t2: -22.1421 + 51.9411i

t3: -4.72831 + 82.9428i

t4: 20 + 50i

t5: 52.5074 + 9.44519i

t6: 78.7107 + 18.7696i

t7: 81.8089 + 16.356i

t8: 60 - 2i

t9: 29.0566 + 3.54352i

t10: 6.14214 - 15.9411i

t11: -6.5854 - 57.4869i

t12: -20 - 50i

t13: -41.1937 - 34.901i

t14: -62.7107 - 54.7696i

t15: -70.4952 - 41.8119i

Figure 3: Signal timeline (side-on) and complex plane (front-on) viewpoints

The next step is to rotate [2] and then split the signal into two separate signals derived from the real components and imaginary components respectively (i.e., {-2, -21.9123, ...} and {-60, -40.3703, ...}).

A Discrete Fourier Transform is now applied to each signal to produce their spectrums.[3][4] The first generated spectrum is:

f1: 50i

f2: 18i

f3: 12

f5: -14

The second generated spectrum is:

f1: -60-30i

f2: 8i

f3: -10i

There are eight distinct real numbers across both spectrums which can be arranged into four complex parameters, as required!

p1: 50 - 30i

p2: 18 +  8i

p3: 12 - 10i

p4: -14 - 60i

To check these parameters are sufficient to generate the elephant in Figure 1, the inverse procedure can be performed. First, the components of the four parameters specify the two spectrums above. An Inverse Discrete Fourier Transform is then applied to each spectrum to produce their respective signals. The real values of the two signals can then be combined into the original complex signal (and the inverse rotation applied) for the elephant in Figure 1.

One further (fifth) parameter is needed to add some elephant dynamics. The Mayer paper uses the number 40 to specify the x-coordinate of the base of the elephant's trunk (thus the coordinates to the right can be wiggled) and uses the number 20 to specify both the x and y coordinates of the elephant's eye. See the references in my earlier post for implementations of those features.

I'll end here with an apt paraphrase of Einstein: [5]

"Everything should be made as simple as possible (but not simpler)."

--

[1] See Drawing an elephant with four complex parameters - Mayer, Khairy, Howard, 2010.

[2] Note that the imaginary numbers have been negated and then the real and imaginary numbers swapped. This is, in effect, a quarter clockwise rotation of the signal which could alternatively be applied by multiplying the complex signal by i. The rotation isn't actually necessary to produce four parameters but, if omitted, the parameter values will be different from those given in the Mayer paper. The final four parameters without the rotation would be {30 + 50i, -8 + 18i, 10 - 12i, -60 + 14i}.

[3] Scaling factors have been omitted. When testing this using Microsoft Excel's Fourier Analysis tool, a scaling factor of 1/16 was needed for the DFT and 16 for the inverse DFT.

[4] Negative frequencies and zero amplitude frequencies have been omitted. A negative frequency means that an epicycle rotates clockwise instead of counter-clockwise. In this instance, the negative frequencies are the complex conjugates of the positive frequencies and don't affect the results.

[5] "It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience." - Albert Einstein, "On the Method of Theoretical Physics", The Herbert Spencer Lecture, 1933.

Visualizing von Neumann's elephant

Figure 1: This is not an elephant

John von Neumann once remarked to fellow physicist Enrico Fermi: [1]

"With four parameters I can fit an elephant, and with five I can make him wiggle his trunk."

Von Neumann was pointing out the danger of relying on too many input parameters to model a data set - which may then fail to fit additional data or predict future observations.

Figure 2: 128 sample points

Consider the elephant image in Figure 1. How might we model it in order to draw it programmatically?

One approach would be to find a number of points on the green line, as per Figure 2, and then join the points with straight lines.

Figure 3: Satellite path in green

However the approach I'm going to take is to draw the elephant using circles or, more specifically, epicycles.

An epicycle is a circle that moves on the perimeter of another circle and is famously associated with Ptolemaic astronomy. Per Figure 3, imagine the Earth's orbit around the Sun as a large circle and the moon's orbit as a smaller circle on that large circle. Then consider, in turn, a satellite orbiting the moon and you have the idea of epicycles and the complicated absolute path that the satellite can take through space.[2]

The key insight is that the elephant drawing in Figure 1 is, in a sense, just like the complicated satellite path. It also can be represented as a series of circles moving on circles over time. The magic of transforming the set of sample points in Figure 2 into a set of spinning circles is achieved via a Fourier Transform. Figure 4 below shows the (partial) result of applying that transformation.

Figure 4: Drawing an elephant from 128 epicycles (zoomed-in detail on right)

The larger circles (with their radial arrow identifying the present position of their orbiting satellite) contribute the broad strokes of the drawing, so-to-speak, while the smaller circles provide the finer detail.

So can we use less than 128 epicycles? Certainly. The next step is to remove the circles that have minimal effect on the shape of the elephant. These will generally be the smaller circles. Here are the results.[3]

Figure 5: (top row) 50 epicycles, 20 epicycles, (bottom row) 16 epicycles, 8 epicycles

With fifty epicycles, the drawing is virtually indistinguishable from the original image, whereas eight epicycles is about as far as one can reduce to while still retaining recognizable elephant features.[4]

The next step is to figure out how to specify those eight epicycles with just four parameters. That will be explored in my next post.

References:

Drawing an elephant with four complex parameters - Mayer, Khairy, Howard, 2010

The Noisy Elephant - Lydia Nemec

How to fit an elephant - John D. Cook

A Winking Pink Elephant - Neil Gunther

https://github.com/jramirezpr/fourier-elephant - Juan Carlos Ramirez

--

[1] A meeting with Enrico Fermi (subtitled "How one intuitive physicist rescued a team from fruitless research.") - Freeman Dyson, Nature, 2004

'“There are two ways of doing calculations in theoretical physics”, [Fermi] said. “One way, and this is the way I prefer, is to have a clear physical picture of the process that you are calculating. The other way is to have a precise and self-consistent mathematical formalism. You have neither. ... To reach your calculated results, you had to introduce arbitrary cut-off procedures that are not based either on solid physics or on solid mathematics."

...

In desperation I asked Fermi whether he was not impressed by the agreement between our calculated numbers and his measured numbers. He replied, “How many arbitrary parameters did you use for your calculations?” I thought for a moment about our cut-off procedures and said, “Four.” He said, “I remember my friend Johnny von Neumann used to say, with four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” With that, the conversation was over.'

[2] The term planet means "wanderer" in Greek, expressing the fact that they are seen to move across the sky relative to the background stars.

[3] The "8 epicycles" result comes from the Mayer paper and involves some adjustments to the remaining epicycles.

[4] Drawing with just one circle would produce a circular elephant.