Visualizing linear algebra: Change of basis

Figure 1: Alternative basis vectors

This is Part 7 in a series on linear algebra [1].

Any given vector can be understood as the scaling of the unit vectors i-hat and j-hat. These special vectors are the standard basis vectors in a coordinate system.

However it is also possible to use different basis vectors. In Figure 1, the basis vectors b₁ and b₂ point in different directions and have different lengths to i-hat and j-hat.

Figure 2: Alice and Bobs' coordinate systems

Suppose that Alice uses the standard basis vectors i-hat and j-hat while Bob uses the alternative basis vectors b₁ and b₂. While Alice and Bob are looking at the same vectors in space, they can be considered to be using different languages to refer to them.

In Figure 2, Alice would describe b₁ with the vector coordinates [2;1] and b₂ with the vector coordinates [-1;1].[2] Whereas from Bob's perspective, b₁ and b₂ have coordinates [1;0] and [0;1]. They are what define the meaning of the coordinates [1;0] and [0;1] in his system. To reiterate, both Alice and Bob are looking at the same vectors in space, but they use different words and numbers to describe them.

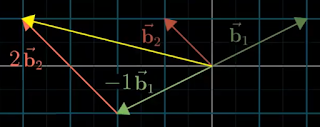Figure 3: Vector [-1;2] in Bob's system

To translate between Alice and Bobs' coordinate systems, consider Figure 3. Suppose Bob describes a vector with coordinates [-1;2] in his system. That is, b₁ is scaled by -1 and b₂ is scaled by 2 as represented by the yellow arrow. From Alice's perspective, the coordinates for b₁ and b₂ in her system can be similarly scaled to describe the vector in her system. That is:

-1[2] + 2[-1] = [-4]

  [1]    [ 1]   [ 1]

Note that this is just matrix-vector multiplication with a matrix whose column vectors represent Bob's basis vectors in Alice's language. That is:

[2 -1][-1] = -1[2] + 2[-1] = [-4]

[1  1][ 2]     [1]    [ 1]   [ 1]

In effect, a matrix whose column vectors represent Bob's basis vectors can be thought of as a transformation that moves Alice's basis vectors, i-hat and j-hat, to Bob's basis vectors, b₁ and b₂. So the vector [-1;2] is a certain linear combination of Alice's basis vectors (-1î + 2ĵ ). The resulting vector after the transformation will be that same linear combination but of the new basis vectors (-1b₁ + 2b₂). This transformation, in essence, enables Alice to describe vectors in Bob's language.

It is similarly possible for Bob to describe vectors in Alice's language. This requires taking the inverse of the matrix which corresponds to playing the transformation backwards. The inverse of the matrix is:

[2 -1]^-1 = [ 1/3 1/3]

[1  1]     [-1/3 2/3]

Let's go in the other direction, taking the vector that Alice describes in her language above as [-4;1] and describe it in Bob's language:

[ 1/3 1/3][-4] = -4[ 1/3] + 1[1/3] = [-1]

[-1/3 2/3][ 1]     [-1/3]    [2/3]   [ 2]

The result is [-1;2] in Bob's language which is verified by the yellow arrow in Figure 3.

That is how to translate the descriptions of individual vectors back and forth between coordinate systems. The matrix whose columns represent Bob's basis vectors but written in Alice's coordinates translates vectors from Bob's language into Alice's. And the inverse matrix does the opposite.

Linear transformations involving matrices can also be described in different coordinate systems. For example, a 90° counterclockwise rotation can be described in Alice's system as:

[0 -1]
[1  0]

That is, i-hat ends up at coordinates [0;1] and j-hat ends up at coordinates [-1;0]. To translate this into Bob's system, first consider a vector in Bob's language, say, the vector [-1;2] from above. That vector needs to be translated to Alice's language using the change of basis matrix, then the rotation applied in Alice's language, then translated back to Bob's language using the inverse change of basis matrix. This can be represented, from right-to-left, as:

[2 -1]^-1[0 -1][2 -1][-1]
[1  1]  [1  0][1  1][ 2]

This transformation sequence will work for any vector in Bob's language. The product of the three matrices is:

[2 -1]^-1[0 -1][2 -1] = [1/3 -2/3]

[1  1]  [1  0][1  1]   [5/3 -1/3]

If Bob applies this composition matrix to a vector in his system, it will return the rotated version of that vector expressed in his coordinate system. For example:

[1/3 -2/3][1] = [-1]

[5/3 -1/3][2]   [ 1]

With an expression like A^-1MA , the middle matrix represents a transformation M as one person sees it, the outer matrices indicate the shift in perspective, while the full matrix product represents a transformation M as someone else sees it.

Next up: eigenvectors

--

[1] The figures and examples of the posts in this series are based on the Essence of Linear Algebra series by 3Blue1Brown.

[2] The notation [x;y] using a semicolon indicates a column vector.