 |
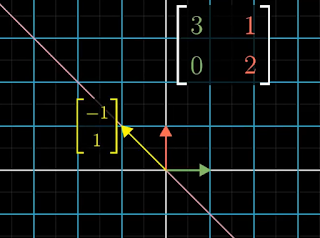
| Figure 1: Before transformation |
A vector that remains on its span [2] when a linear transformation is applied to it is termed an eigenvector of that transformation. The amount that it is scaled is called an eigenvalue.
For example, Figure 1 shows a yellow arrow that will be transformed by the indicated matrix. The purple line is the span of the yellow arrow.
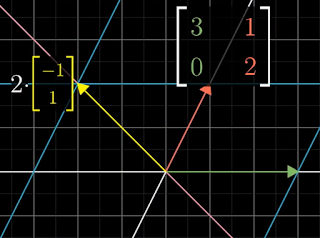 |
| Figure 2: After transformation |
Notice that i-hat is also an eigenvector and its eigenvalue is 3 (i.e., it is scaled by 3). However j-hat has not remained on its span, so it is not an eigenvector of the transformation.
Any vector that lies on the span of either the yellow arrow or the green arrow is an eigenvector and it will also have the eigenvalues 2 and 3 respectively. Any vector, such as the red arrow, that does not lie on either of those spans will be rotated off the line that it spans.
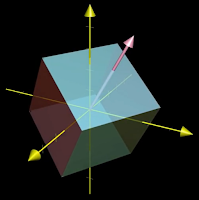 |
| Figure 3: 3D rotation around an axis |
For one example of where finding an eigenvector is useful, consider a 3D dimensional rotation as in Figure 3. If you can find an eigenvector for that transformation, a vector that remains on its own span, then you have found the axis of rotation. For rotations the eigenvalue is always 1 since the length of the vector remains the same.
Note that the columns of a matrix describe the landing spots for the basis vectors. However, as illustrated by the 3D rotation, finding the eigenvectors and eigenvalues describes what the transformation does independent of the particular basis vectors used.
An eigenvector equation can be represented as:
Av = λv
where A is the matrix representing a transformation, v is the eigenvector and λ (lambda) is the corresponding eigenvalue (a number). This expression says that the matrix-vector product (A times v) gives the same result as just scaling the eigenvector v by some value λ. So finding the eigenvectors and their eigenvalues of a matrix A comes down to finding the values of v and λ that make this expression true.
The first step is to convert the right-hand-side of the equation so that it represents a matrix-vector product like the left-hand-side of the equation. This is done by multiplying λ by the identity matrix I, as follows:
Av = (λI)v
Av - λIv = 0
(A - λI)v = 0
det(A - λI) = 0
[3 1]
[0 2]
Now think about subtracting a variable amount λ from each diagonal entry:
[0 2] [0 1] [ 0 2-λ]
The goal is to find any values of λ that will make the determinant of the matrix zero. That is:
det([3-λ 1]) = ad - bc = (3-λ)(2-λ) - 1*0 = (3-λ)(2-λ) = 0
[ 0 2-λ]
So when λ equals 2 or 3, the matrix (A - λI) transforms space onto a line. That means there are non-zero vectors v such that (A - λI) times v equals the zero vector. Recall the reason we care about that is because it means Av = λv. That is, the vector v is an eigenvector of A.
To figure out the eigenvectors that have one of these eigenvalues, plug that value of λ into the matrix and then solve for which vectors this diagonally-altered matrix sends to zero. Solving with λ = 2:
[3-2 1][x] = [1 1][x] = x[1] + y[1] = [x+y] = [0]
[ 0 2-2][y] [0 0][y] [0] [0] [ 0] [0]
[3-3 1][x] = [0 1][x] = x[0] + y[ 1] = [ y] = [0]
[ 0 2-3][y] [0 -1][y] [0] [-1] [-y] [0]
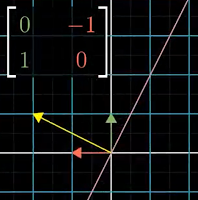 |
| Figure 4: 90° rotation |
det([-λ -1]) = (-λ)(-λ) - -1*1 = 0
[ 1 -λ]
= λ2 + 1 = 0
∴ λ = i or λ = -i
The only roots of that polynomial are the imaginary numbers i and -i. Assuming we are only looking for real number solutions, there are no eigenvectors for that transformation. However note that eigenvalues that are complex numbers generally correspond to some kind of rotation in the transformation.
Whenever a matrix has zeroes everywhere other than the diagonal, it is called a diagonal matrix. The way to interpret this is that all the basis vectors are eigenvectors with the diagonal entries of the matrix being their eigenvalues. That is, a diagonal matrix simply scales the basis vectors. A diagonal matrix can be represented as a vector times the identity matrix I. For example:
[-1 0] = [1 0][-1]
[ 0 2] [0 1][ 2]
Therefore, whenever we want to apply a matrix multiplication to a diagonal matrix, it is the same as applying a matrix-vector multiplication, converting an O(N2) operation into O(N).
If a transformation has enough eigenvectors such that you can choose a set that spans the full space, then you can change your coordinate system so that these eigenvectors are your basis vectors. For example, using the eigenvectors for the matrix from Figure 1 as the change of basis matrix (the green and yellow arrows):
[1 -1]-1[3 1][1 -1] = [3 0]
[0 1] [0 2][0 1] [0 2]
This new matrix is guaranteed to be diagonal with its corresponding eigenvalues down that diagonal. The new basis is called an eigenbasis with Figure 5 showing the change of basis. Applying the transformation will scale the new basis vectors by those eigenvalues, that is, the green arrow by 3 and the yellow arrow by 2.
Whenever a matrix has zeroes everywhere other than the diagonal, it is called a diagonal matrix. The way to interpret this is that all the basis vectors are eigenvectors with the diagonal entries of the matrix being their eigenvalues. That is, a diagonal matrix simply scales the basis vectors. A diagonal matrix can be represented as a vector times the identity matrix I. For example:
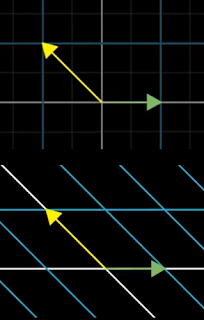 |
| Figure 5: Change of basis |
[ 0 2] [0 1][ 2]
If a transformation has enough eigenvectors such that you can choose a set that spans the full space, then you can change your coordinate system so that these eigenvectors are your basis vectors. For example, using the eigenvectors for the matrix from Figure 1 as the change of basis matrix (the green and yellow arrows):
[1 -1]-1[3 1][1 -1] = [3 0]
[0 1] [0 2][0 1] [0 2]
Next up: vector spaces
[1] The figures and examples of the posts in this series are based on the Essence of Linear Algebra series by 3Blue1Brown.
[2] A vector that remains on its span either points in the same direction or points in the opposite direction (the negative direction).
No comments:
Post a Comment